Table of Contents
概要
SIFT(Scale Invariant Feature Transform)で使われるスケール空間の解説です。
SIFTについては、例えば Introduction to SIFT(OpenCV)
画像の特徴は、スケールを変えることによって明確になることがあります。
以下の図は、文字通りに言えば直線ではありませんが、遠くから見れば直線になります。
実際にカメラを引くことができればもちろんよいのですが、与えられた画像からそのような特徴を抽出するにはどうすればよいか、ということでスケール空間という考え方があります。
フィルタをかけてぼかす(スムージングする)ことで細かな変化が消え、遠くから見た特徴が得られるというもので、スムージングの度合いでスケールを表現します。
The motivation at the heart of this approach is that increased blurring will cause unimportant details to blend in with the background, thus focusing attention on the structure and interrelations of the more prominent features.
参考文書[1] A. Definitions and Notation
スケールという言葉に惑わされがちですが、与えられた画像以上の情報は得られません。木の画像をスケーリングしたら森の画像になるかというとそんなわけはなく、木をズームアウトするだけです。また、ズームインもできません。
スムージング=ガウシアンフィルタと思われるかもしれませんが、ここでは以下の性質を持つものをスムージングと呼ぶことにします。
- フィルタ後の極値の数は、フィルタ前の極値の数よりも大きくならない
どのような入力に対しても、というのがポイントです。
このようなスムージングの仕方はひとつではないのですが、いくつかの直観的な条件を課すとガウシアンフィルタだけが残ります。つまり、ガウシアンフィルタが最も理想的な性質を持つスムージングであるということになります。
- 線形であること(linear)
- 平行移動に対して不変であること(shift invariant)
- 回転に対して不変であること(rotationally invariant)
- 重ねがけができること(recursivity)
- スケール不変であること(scale invariant)
これらの条件からガウシアンフィルタが導かれることを示すのが目標です。
なお、画像は2次元ですが、簡単にするために1次元の信号(音声などのイメージ)で考えます。
2次元の場合も同じ結論になります。
スケール空間表現
フィルタ K_t を信号 f にかけることで、新たな信号(関数) K_t f が得られます。パラメータ t を連続的に変えることで、信号の系列 \{K_t f\} が得られます。この \{K_t f\} を、信号 f のスケール空間表現(scale space representation)と言います。
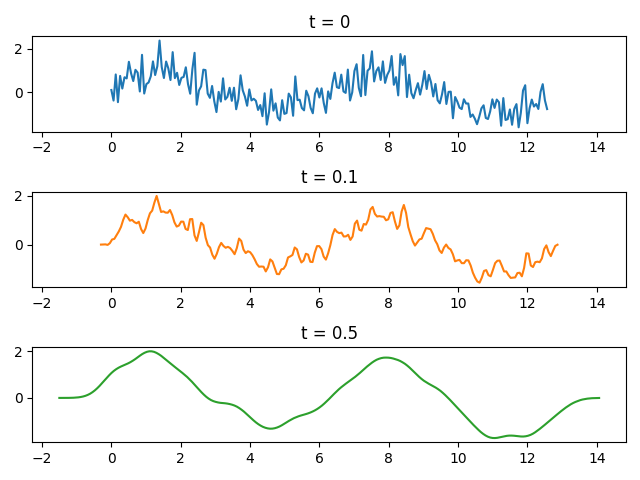
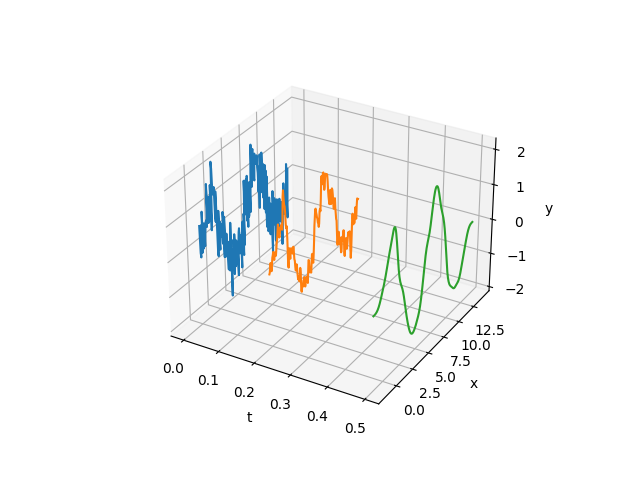
スケール空間の条件
線形であること
ふたつの信号を混ぜてからスムージングするのと、スムージングしたもの同士を混ぜるのは同じ結果になるということです。
K_t(f + g) = K_t f + K_t g
そこで、K_t は積分で表されるものとします。
(K_t f)(x) = \int_{-\infty}^\infty k_t(x, y)f(y)dy関数の変換を積分で表すのは一般的なことであって、k_t(x, y) = e^{-ixy} ならフーリエ変換、k_t(x, y) = e^{-xy} ならラプラス変換です。その他、様々な変換があります。
ガウシアンフィルタは k_t(x, y) = e^{-(x - y)^2/4t} です。
平行移動に対して不変であること
これは、スムージングしたものを平行移動しても、平行移動してからスムージングしても、同じ結果になるということです。結論から言うと、線形でシフト不変な演算は畳み込みで表されるのですが、もう少し詳しく説明します。
スムージングしたもの (K_t f) を平行移動すると
(K_t f)(x - a) = \int k_t(x - a, y)f(y)dy
平行移動した関数 f'(x) = f(x - a) をスムージングすると
\begin{align*}
(K_t f')(x) &= \int k_t(x, y)f'(y)dy \\
&= \int k_t(x, y)f(y - a)dy \\
&= \int k_t(x, y + a)f(y)dy
\end{align*}したがって、任意の a に対して k_t(x - a, y) = k_t(x, y + a) となります。
これより、k_t は (x,y) 平面の直線 x - y = c 上で同じ値を取ります。実際、x - y = c 上の点 (x, y), (x', y') に対して x' - x = a とすると
k_t(x, y) = k_t(x' - a, y) = k_t(x', y + a) = k_t(x', y')
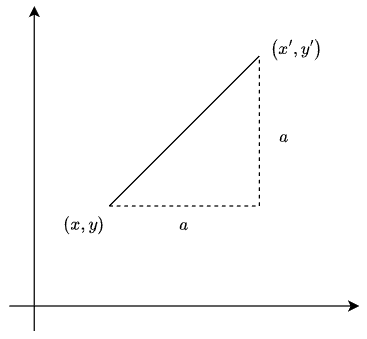
これは、k_t(x,y) が (x - y)^2 や x^{x - y} のような形の x - y の関数であることを意味します。
k_t(x, y) = k_t(x - y) \\
(K_t f)(x) = \int_{-\infty}^\infty k_t(x - y)f(y)dyこれは畳み込みの定義そのものです。
そこで、k_t は一変数の関数 k_t(x) として、以下の条件を満たすものとします。
\int_{-\infty}^\infty k_t(x) dx = 1 \tag{1}これは、ざっくり言うと畳み込みをした後も信号の総量が変わらない、どこかが下がればどこかが盛り上がるということです。信号 f(x) の積分は有限とは限りませんが、有限であれば
\begin{align*}
\int_{-\infty}^\infty K_t f(x) dx &= \int_{-\infty}^\infty \left( \int_{-\infty}^\infty k_t(x - y) f(y) dy \right) dx \\
&= \int_{-\infty}^\infty \left( \int_{-\infty}^\infty k_t(x - y) dx \right) f(y) dy \\
&= \int_{-\infty}^\infty f(y) dy
\end{align*}回転に対して不変であること
スムージングしたものを回転しても、回転してからスムージングしても、同じ結果になるということです。1次元では、
k_t(x) = k_t(-x)
であることを意味します。
2次元の場合は、k_t は原点からの距離の関数 k_t(x,y) = k_t(r)\ (r = \sqrt{x^2 + y^2}) になります。
重ねがけができること
ここまでは、異なるパラメータ t,s(t \ne s) に対して K_t と K_s は何の関連も仮定していませんでした。
この条件は、スムージングを続けて行うのと、一度にスムージングするのは同じ結果になるということで
K_t(K_s f) = K_{t + s} fを意味します。スケールの足し算ができると言うこともできます。
また、
K_0 f = f \\
\lim_{t \to +0} K_t f = fも満たすものとします。
畳み込みはフーリエ変換するとかけ算になるので
\hat{k}_t(\omega) \cdot \hat{k}_s(\omega) = \hat{k}_{t + s}(\omega)一般に
f(x)f(y) = f(x + y)
を満たす関数は f(x) = e^{ax} なので、\hat{k}_t(\omega) を t の関数とみなせば
\hat{k}_t(\omega) = e^{-g(\omega)t} \tag{2}の形に書くことができます。
逆フーリエ変換により
k_t(x) = \frac{1}{2\pi}\int_{-\infty}^\infty e^{-g(\omega)t} e^{i \omega x}\ d\omegaとなるので、g(\omega) を求める問題に帰着します。
偶関数のフーリエ変換は偶関数なので、g(\omega) も偶関数です。
\int_{-\infty}^\infty |k_t(x)|^2 dx = \int_{-\infty}^\infty|\hat{k}_t(\omega)|^2 d\omegaであることと(1)より
\lim_{\omega \to \infty} \hat{k}_t(\omega) = 0 \tag{3}ガウシアン関数 e^{-x^2} のフーリエ変換は e^{-\omega^2} の形なので、g(\omega) = \omega^2 であることが予想されます。
スケール不変であること
k_t の形が t の値によらず”qualitatively identical”であることを言っています。
This means that there should exist a fixed kernel function (or “parent-kernel”) \phi such that at different levels of the scale-parameter, k_t is simple rescaling of this parent-kernel by means of a rescaling-function
参考文書[1] D. The Principle of Scale Invariance
これは、”parent-kernel” \phi(x) と単調増加関数 \psi(t) を用いて
k_t(x) = \frac{1}{\psi(t)}\phi\left(\frac{x}{\psi(t)}\right) \tag{4}と表される、つまり k_t は \phi(x) を横に広げたものであるということです。
\sin x と \sin 2x のグラフを考えればイメージできると思います。
スケールを大きくすると、ある意味で画像が崩れていきますが、スケール不変は崩れ方が同じであることを言っています。一方、重ねがけは崩れる速さに関する主張です。
極値の数が大きくならないこと
これは k_t(x) が負の値を取らないことを意味します。これを直接示すのは簡単ではないので、反例を考えます。
インパルス信号は、ディラックのデルタ関数で表される、原点に鋭いピークを持つ関数です。
\delta(x) = \begin{cases}
\infty & (x = 0) \\
0 & (x \ne 0)
\end{cases}デルタ関数の計算の仕方を見れば明らかですが、インパルス信号と k_t(x) の畳み込みは k_t(x) 自身になります。
k_t(x) * \delta(x) = \int_{-\infty}^\infty k_t(x - y) \delta(y) dy = k_t(x)インパルス信号の極値は原点にひとつのみであり、k_t(x) は負の値を取るなら最低2個の極値を持ちます。すべての信号に対して、というスムージングの性質に反するので、負の値は認められません。
k_t(x) の導出
少々長くなりますが、ここから k_t(x) を求めていきます。
以下の順にたどっていきます。
- g(\omega) = a|\omega|^\alpha\ (a, \alpha > 0) であること
- \alpha は偶数であること
- \alpha = 2 であること
- k_t(x)
g(\omega) = a|\omega|^\alpha であること
(2)と(4)から g と \psi の関係がわかります。具体的には、g と \psi^{-1} が同じ関数形になり、そこから
g(\omega)g(\omega') = g(1) g(\omega\omega') \tag{5}となることを示します。
g(1) の項が奇妙な印象ですが、g(\omega) = a|\omega|^\alpha は実際 g(1) = a として(5)を満たします。
絶対値 |\cdot| は偶関数であるために必要です。
\alpha < 0 とすると \omega \to \infty で \hat{k}_t(\omega) = e^{-a |\omega|^\alpha t} \to 1 なので(3)に反します。
a < 0 とすると \hat{k}_t(\omega) \to \infty となり、これも(3)に反します。
(5)を求めるために、(4)に \psi(t_1) = 1 となる t_1 を代入すると
k_{t_1}(x) = \frac{1}{\psi(t_1)} \phi\left(\frac{x}{\psi(t_1)}\right) = \phi(x)(2)より \phi(x) のフーリエ変換が求まり、
\hat{\phi}(\omega) = \hat{k}_{t_1}(\omega) = e^{-g(\omega)t_1} \tag{6}(このような形に書けるというだけで、g(\omega) も t_1 も未知のままです)
任意の t については、フーリエ変換の定数倍の性質(Wikipedia)
h(x) = f(ax) \\
\hat{h}(\xi) = \frac{1}{|a|}\hat{f}\left(\frac{\xi}{a}\right)を(4)に対してうまく使ってやると
\hat{k}_t(\omega) = \hat{\phi}(\psi(t) \omega)となります。k_t(x) が\phi(x) の定数倍 (a = 1 / \psi(t)) であることに注意すればわかります。
(6)の \omega に \psi(t) \omega を代入して
\hat{k}_t(\omega) = e^{-g(\psi(t) \omega) t_1}これと(2)の
\hat{k}_t(\omega) = e^{-g(\omega) t}を比較すると
g(\omega)\ t = g(\psi(t) \omega)\ t_1
\omega' = \psi(t) > 0 とおくと t = \psi^{-1}(\omega') であり
g(\omega)\psi^{-1}(\omega') = g(\omega'\omega) t_1 \tag{7}\omega = 1 を代入すると
\psi^{-1}(\omega') = \frac{t_1}{g(1)} g(\omega')t_1 と g(1) は定数なので、\psi^{-1} と g が同じ関数形であることが示されました。
これを(7)に代入すれば、(5)が得られます。
これより、
\hat{k}_t(\omega) = e^{-a|\omega|^\alpha t}となります。
\alpha は偶数であること
k_t(x) も \hat{k}_t(\omega) の逆フーリエ変換として求まってはいるのですが、残念ながら \alpha = 2 などの例外を除いて、これを解析的な形で表すことはできません。\hat{k}_t(\omega) の形から k_t(x) の性質を探ることになりますが、これは簡単ではないので省略します。ざっくり言うと
\alpha が偶数でない場合、t \to 0 で K_t f \to f に(必ずしも)なりません。
ちなみに \alpha が偶数の場合は
\lim_{h \to 0} \frac{K_{h} f - f}{h}が存在し、任意の t に対して
\lim_{h \to 0} \frac{K_{t+h} f - K_t f}{h} = \lim_{h \to 0} \frac{K_t(K_h f - f)}{h} = \lim_{h \to 0} \frac{K_{h} - I}{h} K_t fとなります。
K_t f = f(x, t) のように表すと、左辺は t に関する偏微分 \partial f / \partial t とみなすことができます。
\frac{\partial f}{\partial t}(x, t) = L f(x, t) \\
L = \lim_{h \to +0} \frac{K_{h} - I}{h}これは f(x) = f(x, 0) を初期条件とする偏微分方程式で、その解は
f(t, x) = e^{tL} f \\
e^{tL} = \sum_{n=0}^\infty \frac{t^n}{n!} L^nと表されます。いわゆる発展方程式です。
この辺りをきちんと理解するには演算子の考え方に慣れる必要があるのですが(演算子の極限をどうやって定義するか等)、きちんと定義すれば実数と同じような計算ができるようになります。L を半群(semigroup) \{K_t\} の無限小生成演算子(infinitesimal generator)と言ったりもします。
\alpha = 2 であること
\alpha が 2 よりも大きい場合、k_t(x) は負の値を取ることを示します。
フーリエ変換の微分(≠微分のフーリエ変換)は
\frac{d}{d\omega} \hat{k}_t(\omega) = -i \int x k_t(x) e^{-i \omega x} dx \\
\frac{d^2}{d\omega^2} \hat{k}_t(\omega) = \int x^2 k_t(x) e^{-i \omega x} dxであり、\omega = 0 で微分可能なら
\hat{k}_t^{(2)}(0) = \int x^2 k_t(x) dx\alpha > 2 の場合、\hat{k}_t(\omega) = e^{-a|\omega|^\alpha t} = e^{-a\omega^\alpha t} を二回微分するとどちらの項にも \omega が現れるので \hat{k}_t^{(2)}(0) = 0 になります。
これより、
\int x^2 k_t(x) dx = 0
k_t(x) \ge 0 なら x^2 k_t(x) \ge 0 なので、積分が 0 になるためには k_t(x) \equiv 0(すべての点で 0 ※)でなければならず、矛盾します。
※正確に言うと、k_t(x) = 0 a.e.(almost everywhere、ほとんどすべての点で0)です。
k_t(x)
a が変われば異なるスケール空間表現になりますが、本質的にはどれも同じなので、a = 1 とします。フーリエ変換の表からもわかる通り
\begin{align*}
k_t(x) &= \frac{1}{2\pi}\int e^{-\omega^2t} e^{i \omega x} d\omega \\
&= \sqrt{\frac{1}{4 \pi t}} e^{-x^2 / 4t}
\end{align*}これで k_t(x) が求まりました。
\phi(x) = \sqrt{\frac{1}{4 \pi}} e^{-x^2 / 4} \\
\psi(t) = \sqrt{t}とおくと、実際に(4)の形になっていることがわかります。
t = \sigma^2 / 2 とおくと
k_t(x) = \sqrt{\frac{1}{2 \pi \sigma^2}} e^{-x^2/2\sigma^2}これは標準偏差 \sigma の正規分布です。
Laplacian of Gaussian
少し計算しないといけないですが、\alpha = 2 の場合は
L f = \lim_{h \to +0} \frac{K_h f - f}{h} = f^{(2)}(x)つまり、
L = \frac{d^2}{dx^2}という微分演算子になります。2次元の場合はラプラシアン \nabla^2 = \partial^2 / \partial x^2 + \partial^2 / \partial y^2 で、いわゆる拡散方程式です。
\frac{\partial f}{\partial t} = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2}ガウシアンフィルタに続けてラプラシアンフィルタをかける、いわゆるLaplacian of Gaussian(LoG)は、スケール方向の変化の大きさを計算しているということになります。
まとめ
画像のスケール空間を定義し、ある一定の条件を満たすものはガウシアンフィルタだけであることを(1次元で)示しました。このスケール空間はある種の画像の特徴を抽出するのに有効であり、SIFTへとつながっていきます。
参考文書
[1] An Extended Class of Scale-Invariant and Recursive Scale Space Filters