ガロア体(Galoir field)とは、実数のような四則演算ができて、要素数が有限のものです。有限体(finite field)と言うこともあり、個人的には有限体の方がしっくりきます。なぜこんなものが必要かと言うと、
体というのは有理数の全体や、実数の全体のように、その中で四則演算が普通に出来る集合のことで、しばらくの間は一般体の代りに有理数の全体を考えていてもよかろう。しかし一般にすると定理の適用範囲が広くなり、内容が豊かになるのである。
鈴木道夫 群論(1977)
積分方程式の理論からヒルベルト空間が生まれたように、有理数や実数を体(field)という形に一般化することができ、それによりガロア体の存在が明らかになります。一般的な理論はすべての体に適用でき、ガロア体は暗号や誤り訂正などへの応用へと広がっていきます。
ガロア体を一言で言うと
- 要素数は p^n(p は素数)であり、GF(p^n) と表される。
- GF(p) は整数、GF(p^n)\ (n \ne 1) は多項式のように演算する。
一番簡単なガロア体は GF(2) = \{0, 1\} で、以下のようになります。
1 + 1 = 0 \\ 1 \times 1 = 1
ガロア体を応用で使う人向けに、基本的な考え方と多項式としての計算の仕方を解説します。
Table of Contents
最小のガロア体
p を素数として
\mathbb{Z}_p = \{0, 1, \cdots, p - 1\}は、整数の足し算とかけ算に関してガロア体になります。ただし、p で一周するものとします。
\mathbb{Z}_5 = \{0, 1, 2, 3, 4\} であれば
4 + 1 = 0\ (4 = -1) \\ 3 \times 4 = 12 = 2
のようになります。
なぜ素数に限定するかと言うと、p が素数でなければ、例えば \mathbb{Z}_6 では 3 \times 2 = 6 = 0 となってしまうからです。
これは、数の基本的な性質
ab = 0 \implies a = 0\ \text{or}\ b = 0を満たしていないので不合理です。
\mathbb{Z}_p は、任意の a\ (\ne 0) に対して ab = 1 となる b が存在するので、この b を 1/a = a^{-1} とおいて
c/a = c \cdot a^{-1} = cbとして、割り算を定義できます。
なぜこのような b が存在するかと言うと、
ab = ac \implies a(b - c) = 0 \implies b - c = 0
であることから、a \cdot 1, a \cdot 2, \cdots, a \cdot (p - 1) はすべて異なる p - 1 個の値であり、集合として \{1, 2, \cdots, p - 1\} と一致します。したがって、この中に必ず 1 が存在するからです。
\mathbb{Z}_7 の場合、3 \cdot 5 = 15 = 1 なので 1/3 = 5 であり、2 / 3 = 2 \cdot 5 = 10 = 3 のようになります。
\mathbb{Z}_p は要素数が p のガロア体であり、素体(prime field)と言います。
\sum_{i = 1}^p 1 = 0となる最小のガロア体です。
整数全体 \mathbb{Z} = \{0, \pm 1, \pm 2, \cdots \} はガロア体ではないことに注意してください。これは、要素数が有限でないというのもありますが、割り算が定義できないからです。1 / 2 は整数ではないので、このような演算は認められません。
(有理数や実数まで広げれば定義できます)
割り算が定義できるとは、\mathbb{Z}_p の中の割り算の結果は \mathbb{Z}_p の値になるということです。
性質
a \ne 0,1 に対して a^n \ne a^{n-1} であり、要素数が有限なことから、同じ値をかけ続けるといつかは 1 になります。具体的には、
a^{p - 1} = 1これは整数論におけるフェルマーの小定理そのもので、\mathbb{Z}_7 を例に取ると
3^1 = 3 = 3 \\ 3^2 = 9 = 2 \\ 3^3 = 27 = 6 \\ 3^4 = 81 = 4 \\ 3^5 = 243 = 5 \\ 3^6 = 729 = 1
と、実際にそのようになっていることがわかります。
上記からわかるように、\mathbb{Z}_7 の 0 以外の値は 3^n の形に書くことができます。このように、すべての値を a^n の形に書けるものを巡回群と言い、\mathbb{Z}_7 の乗法群は巡回群であると言います。
一般に、\mathbb{Z}_p の乗法群は巡回群です。
(先走って言うと、これは任意の GF(p^n) に対して成り立ちます)
なお、
n < p \implies a^n \ne 1
とは限らず、例えば \mathbb{Z}_7 では 2^3 = 1 です。
2^1 = 2 \\ 2^2 = 4 \\ 2^3 = 8 = 1
そのため、\mathbb{Z}_7 を 2^n の形に書くことはできません。上記の 3 のように、6 乗で初めて 1 になる値を原始 6 乗根(primitive 6th root of unity)と言います。任意の \mathbb{Z}_p に対して、原始 (p - 1) 乗根が存在します。
その他のガロア体
すべてのガロア体は素体 \mathbb{Z}_p を含みます。どの \mathbb{Z}_p を含むかはガロア体により異なりますが、必ずひとつ含みます。
実際、ふたつのガロア体の共通部分 (\cap) はガロア体である(その中で四則演算が定義できる)ことを利用すれば、すべての部分体(subfield)の共通部分が素体 \mathbb{Z}_p です。
\mathbb{Z}_p を含むガロア体は \mathbb{Z}_p 上のベクトル空間です。これは、成分が \mathbb{Z}_p の値であるベクトルで表されるということで
\boldsymbol{x} = (x_1, \cdots, x_n)\ (x_i \in \mathbb{Z}_p)要素数は必然的に p^n になります。また、要素数が p^n のガロア体はただひとつ存在します。そのため、これを GF(p^n) と表すことができます。\mathbb{Z}_p も GF(p) と書きます。
ベクトル空間として、足し算とスカラー倍はそれぞれ
\boldsymbol{x} + \boldsymbol{y} = (x_1 + y_1, \cdots, x_n + y_n) \\
\lambda \boldsymbol{x} = (\lambda x_1, \cdots, \lambda x_n)\ (\lambda \in GF(p))p = 2 の場合は \lambda = 0, 1 で
\boldsymbol{x} = (x_1, \cdots, x_n)\ (x_i = 0, 1)特に、\boldsymbol{x} + \boldsymbol{x} = 0 です。
繰り返しますが、GF(p^n) は \mathbb{Z}_{p^n} ではありません。
性質
GF(p) と同様、a \in GF(p^n) に対して 1, a, a^2, \cdots はいつかは 1 になります。したがって、GF(p^n) の値はすべて 1 の (p^n - 1) 乗根です。
1 の (p^n - 1) 乗根は (p^n - 1) 次の多項式 x^{p^n - 1} - 1 の根(root)なので、その数は高々 p^n - 1 個です。一方、GF(p^n) の 0 以外の要素の数も p^n - 1 個です。したがって、1 の (p^n - 1) 乗根の全体と集合として一致し、この中に 1 の原始 (p^n - 1) 乗根が存在します。これを a とおくと、
GF(p^n) = \{0, 1, a, a^2, \cdots, a^{p^n - 2}\}つまり、GF(p^n) の乗法群も巡回群になります。
ガロア体のすべての要素の和は 0 になります。これは等比級数の公式から得られます。
a \ne 1 \implies 1 + a + \cdots + a^{p^n - 2} = \frac{1 - a^{p^n - 1}}{1 - a} = \frac{1 - 1}{1 - a} = 0その他、有用な性質として、任意の a,b \in GF(2^n) に対して
\begin{align*}
(a + b)^2 &= a^2 + 2ab + b^2 \\
&= a^2 + b^2
\end{align*}これは 1 + 1 = 2 = 0 であることを利用しているので、p \ne 2 では成り立ちません。
補足
要素数が同じガロア体はただひとつ存在するというのはどういうことか、群と比較すればわかりやすいかもしれません。
群は(足し算がなく)かけ算だけが定義されたものですが、要素数(位数)が同じ群は複数存在します。
例えば \{1, i, -1, -i\}(i は複素数の虚数単位)は位数 4 の巡回群です。特に、i^2 \ne 1 です。
\{1, i, -1, -i\} = \{1, i, i^2, i^3\}一方、
\left\{ \begin{pmatrix}
1 & 0 \\
0 & 1 \\
\end{pmatrix},
\begin{pmatrix}
-1 & 0 \\
0 & 1 \\
\end{pmatrix},
\begin{pmatrix}
1 & 0 \\
0 & -1 \\
\end{pmatrix},
\begin{pmatrix}-1 & 0 \\
0 & -1 \\
\end{pmatrix}
\right\}という行列の集合も、行列のかけ算に関して群になっています。こちらは、どの行列も二乗すると単位行列になるので、前者とは明らかに異なります。
乗法表を見ると
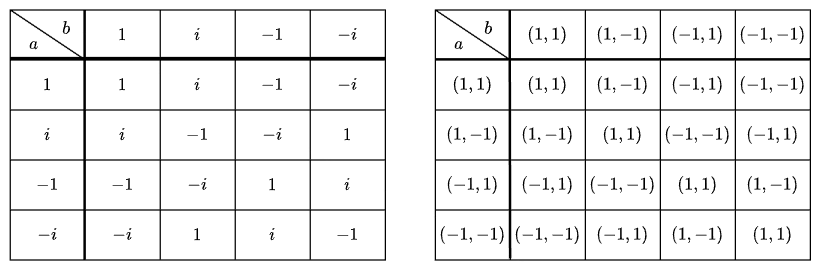
ここで、行列 \begin{pmatrix} a_1 & 0 \\ 0 & a_2 \\ \end{pmatrix} を (a_1, a_2) と表記しています。かけ算 ab の値は、該当する行と列の交差するところになります。
以下の点に注目すると、これらの差異がはっきりします。
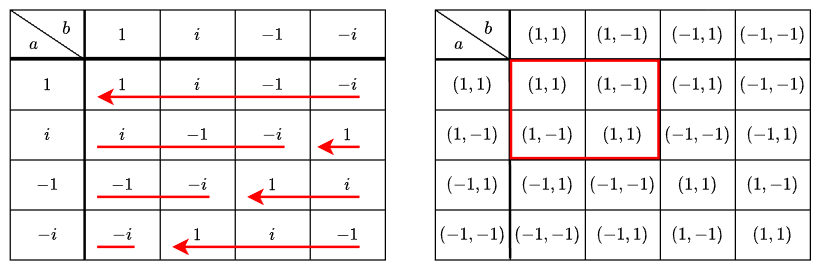
前者は文字通り要素全体を巡回しているのに対し、後者は (1, 1) と (1, -1) で閉じています。
ガロア体ではこのようなことは起きず、要素をうまく並べて同じ記号に置き換えれば、加法表と乗法表はまったく同じになります。両者の区別はできません。
表し方
応用上は p = 2 の場合がほとんどなので、以降 GF(2^n) だけを考えます。
ベクトル(ビット列)
ベクトル空間の成分をビット列とみなすと、GF(2^n) は長さ n のビット列です。1 + 1 = 0 なので
11100 + 00110 = 11010
のようになります。つまり、ガロア体の足し算はビット列の XOR と考えることができます。
ガロア体はベクトル空間なので、ガロア体上の線形写像(行列)を考えることもできます。
多項式
多項式そのものをひとつの数のように考えて、n - 1 次の多項式でガロア体の要素を表すことができます。
a = \sum_{i = 0}^{n - 1} a_i x^i\ (a_i = 0, 1)これを示すのは多項式に関する代数的な知識(環やイデアルなど)が必要になるので省略しますが、足し算とかけ算は多項式の演算になります。
a + b = \left(\sum_{i = 0}^{n - 1} a_i x^i \right) + \left(\sum_{i = 0}^{n - 1} b_i x^i \right) = \sum_{i = 0}^{n - 1} (a_i + b_i) x^i \\
ab = \left(\sum_{i = 0}^{n - 1} a_i x^i \right) \left(\sum_{j = 0}^{n - 1} b_j x^j \right) = \sum_{k = 0} \sum_{i + j = k} a_i b_j x^{i + j}多項式+多項式は多項式、多項式×多項式も多項式なので、いずれもまた GF(2^n) の要素になります。
ただし、次数が n - 1 を超えたときは、n 次の既約多項式の剰余を取ります。
GF(2^2) = GF(4) の場合、x と x + 1 のかけ算は、2 次の既約多項式 x^2 + x + 1 を取り
\begin{align*}
x(x + 1) &= x^2 + x \\
&= (x^2 + x + 1) - 1 \\
&= (x^2 + x + 1) + 1 \\
&= 1
\end{align*}のようになります。GF(2) では -1 = 1 です。
係数を成分とするベクトルで書くと
(1, 0) \times (1, 1) = (0, 1)
ベクトルとしてかけ算を計算するのは直観的ではないので、多項式が便利です。
割り算は \mathbb{Z}_p と同様に定義します。上記の例では 1 / x = x + 1 なので、x で割るということは x + 1 をかけるということです。
なお、GF(2^n) の中の素体 GF(2) = \{0, 1\} は、定数項以外すべて 0 の多項式です。
補足
多項式が既約かどうかは GF(2) で考える必要があり、実数上で考えた場合と必ずしも一致しません。例えば、x^2 + 1 は実数上ではこれ以上因数分解できないので既約ですが、GF(2) 上では x^2 + 1 = (x + 1)^2 なので既約ではありません。
既約かどうかの判定法はいくつかありますが、次数が小さければ総当たりで確認するのが手っ取り早いです。
実装例
GF(2^{128}) は、既約多項式は x^{128} + x^7 + x^2 + x + 1 を用いて表すことができます。
a = \sum_{i = 0}^{127} a_i x^i\ (a_i = 0, 1)x とのかけ算は
\begin{align*}
a \cdot x &= \left(\sum_{i = 0}^{127} a_i x^i \right) \cdot x \\
&= \sum_{i = 0} a_i x^{i + 1} + a_{127} x^{128} \\
&= \sum_{i = 1}^{127} a_{i - 1} x^i + a_{127}(1 + x + x^2 + x^7)
\end{align*}最後の等式は
\begin{align*}
x^{128} &= (x^{128} + x^7 + x^2 + x + 1) - (x^7 + x^2 + x + 1) \\
&= x^7 + x^2 + x + 1
\end{align*}から得られます。GF(2) では -1 = 1 です。
a_{127} = 0 のとき、
a = (a_0, a_1, \cdots) \to a \cdot x = (0, a_0, a_1, \cdots)
これは1ビットの右シフトです。同様に、a_{127} = a_{126} = 0 なら、
a = (a_0, a_1, \cdots) \to a \cdot x^2 = (0, 0, a_0, a_1, \cdots)
a_{127} = 1 のときは、右シフトしたものに 1 + x + x^2 + x^7 を足します。ガロア体の足し算はビット列のXORなので
a \cdot x = (a >> 1) ^ 1110000100 \cdots
^ はビットごとのXOR、1110000100 \cdots は、1 + x + x^2 + x^7 を表すビット列(固定値)です。
void GF2_128_multiply_x(unsigned char* a)
{
int i;
unsigned char a_127 = (a[15] & 0x01);
// a >> 1
for (i = 15; i > 0; i--)
{
a[i] = (a[i] >> 1) | (a[i - 1] << 7);
}
a[0] = a[0] >> 1;
if (a_127 == 1)
{
a[0] ^= 0xe1; // 1 + x + x^2 + x^7
}
}128ビット(16バイト)のビット列なので、16バイトの配列でガロア体を表します。

void print_result(unsigned char* a)
{
int i;
for (i = 0; i < 16; i++)
{
printf("%02x ", a[i]);
}
printf("\n");
}
int main(void)
{
unsigned char a[16];
// a = 1 + x
memset(a, 0, 16);
a[0] = 0xc0;
GF2_128_multiply_x(a);
print_result(a);
// a = 1 + x + x^127
memset(a, 0, 16);
a[0] = 0xc0;
a[15] = 0x01;
GF2_128_multiply_x(a);
print_result(a);
}実行結果
60 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
81 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
それぞれ x + x^2, 1 + x^7 を表します。
まとめ
ガロア体の定義から計算の仕方までを解説しました。ガロア体はベクトルとも多項式ともみなせるという変わった性質を持っています。特に GF(2^n) はベクトル=ビット列であり、ビット演算を使って計算できるので実装が容易です。多項式としての計算に慣れれば、ガロア体を理解したと言ってよいと思います。